Quantum for the curious: 1 - Qubits

 Quantum computing has been in the news lately. Companies, governments, and research labs throughout the world are making significant investments in developing quantum computers. Large companies such as Google, Microsoft, and IBM are racing to build a scalable quantum computer because they believe it will give them a significant edge in high-performance computing. IBM was one of the first companies to offer cloud-based access to a quantum computer for experimentation and education. Google made a splash in October 2019 when they announced that they had achieved "quantum supremacy" for the first time in history. This means that they were able to perform a calculation on their quantum computer, which they estimated would take the fastest supercomputer 10,000 years to complete. Similar announcements have been made since then by teams of researchers in China. While there is a lot of hype around this technology, there are many challenges with building a scalable quantum computer. Quantum computers derive their power from massive parallelism that is made possible by the quantum nature of computational elements in them. But those quantum states are finicky and can be easily destroyed by noise in the system. To mitigate this phenomenon known as decoherence, quantum computing systems have to be isolated from the environment and cooled to very low temperatures. In addition, environmental noise can produce errors that have to be accounted for during computation. This is a major challenge today, but there is a tremendous amount of research being conducted to address this problem and a lot of progress is being made. So there is an expectation that in the next 20-30 years scalable quantum computers will be available to perform a variety of computational tasks. For example, IBM which runs a 65-qubit quantum processor has promised to have a 1000-qubit quantum computer by 2023. It does raise the question of what these quantum computers are going to be good for. There are many potential applications of quantum computers. Simulation of quantum phenomena in chemistry and physics, large-scale optimization problems, and machine learning are some of the well-known applications. But arguably the most dramatic consequence of a quantum computing revolution would be its implications for network communication and security. Public key cryptography is the foundation of secure communication on the internet. Modern eCommerce and internet banking as well as other forms of secure internet communication are all based on TLS, which in turn uses public-key cryptography. The latter is based on the computational hardness of problems such as large factorization. Peter Shor's discovery of an efficient quantum algorithm for integer factorization in 1994 was a showcase of the power of quantum computers to solve classically hard computational problems. But what also got a lot of attention was the realization that a scalable quantum computer would break all of modern public-key cryptography. This has led to a flurry of activity in developing quantum-safe classical cryptography (also known as post-quantum cryptography). Ironically, quantum information theory is also expected to revolutionize network communication by providing provable secure cryptography (via quantum key distribution) and efficient information transfer (via quantum teleportation and super-dense coding).

The Strange World of Quantum

Unlike traditional computers which perform computations using bits, quantum computers use a more exotic unit of information known as a qubit. A qubit (short for a quantum bit) is like the proverbial Schrodinger's cat. Unlike a bit which can take one of two possible values 0 or 1, a qubit can be simultaneously both 0 and 1 when it is not measured and assumes one of the two values 0 or 1 only when it is measured. This is like the cat in Schrodinger's thought experiment, which can be alive and dead at the same time when it is not observed, but decides to be dead or alive when it is measured. This strange description of nature caused enormous discomfort for scientists like Einstein and Schroedinger. In fact, Schroedinger's thought experiment was intended to highlight the absurd implications of quantum theory. If a radioactive atom can be in a superposition of "decayed" and "not-decayed" state at the same time, then the cat whose life depends on the state of the radioactive atom would be in a superposition state of a dead and alive state at the same time. Only when someone chose to open the door and observe the cat does "nature decide" whether the radioactive atom is decayed or not, which would lead to the cat's observed state to be dead or alive. This raised some very unpleasant questions about the nature of reality at the level of elementary particles, which seem to go against our common experience. Such philosophical objections notwithstanding, quantum theory has proved to be an enormously successful and precise theory of nature. The work of scientists such as John Bell and others have demonstrated that nature indeed is quantum in all its glorious strangeness. Moreover, key aspects of this quantum strangeness such as superposition, non-determinism, entanglement, and interference provide significant advantages for computation and communication. This blog post will try to explain these core aspects of quantum information in simple terms. Subsequent posts will cover the topics of quantum computation, its implications for public-key cryptography and quantum communication.  

The Mighty Bit

Much of modern technology is based on digital systems. The fundamental unit of information in such systems is a bit. They are truly the atoms that make up the digital universe. In contrast to analog systems that work with continuously varying quantities, digital systems process discrete quantities of information made out of bits. Bits are so fundamental for information processing because all of the entities of information such as numbers, characters, data structures, memory addresses, and packets transmitted across a network can be encoded in bits. Moreover, using George Boole's laws of logic, bits can be combined and operated upon to perform logical operations. All computer programs ultimately boil down to operations on bits. The discovery of the transistor allowed the efficient realization and manipulation of bits. Very simply, when a transistor switch is on, it allows a current to flow and represents a 1, else it represents a zero. Turning the switch on and off represents bit transitions from, 1 to 0 and vice-versa. Chips made of transistors can switch their bit-states hundreds of thousands a second. More importantly, transistors can be combined to form logic gates to perform operations on bits. Logic gates can be combined to form logic circuits that perform arbitrary computations. Large numbers of transistors known as MOSFETs are combined to form integrated chips (ICs) that can execute computations using logic circuits. The advantage of working with bits (and qubits) is that they abstract away the rules of logic from the physical realizations. So one does not need to know the physics and electronics of computers to understand the rules and algorithms associated with information processing. Let's examine some basic operations one can perform with bits.

Logic Gates

All of these gates can be implemented efficiently using transistors. One thing to note is that while the NOT gate is reversible, all of the other gates are irreversible. We will see later that in contrast to classical logic gates, all quantum gates are reversible. This has deep implications for the physics of computation. 

It also turns out that certain gates are universal meaning that all other gates can be expressed in terms of them. For example, it can be shown that the NAND gate is universal for all classical computation.

Binary Representation of Numbers

Data in computers is represented using an array of bits. For example, a fixed-size array of 32 or 64 bits could be used to represent integers. By using a base 2 (binary) representation one can convert an array of bits into integers. 

Just as one adds integers in decimal notation by "carrying over" a 1 when the sum of the integers in a decimal location is greater than or equal to10, one adds binary digits by performing an XOR (which is the same as addition modulo 2) and carries a 1 over when the sum of two bits in a binary location is greater than or equal to 2. The process of adding two bits and carrying over can be represented by a logic circuit composed of an XOR gate and an AND gate. Such a circuit is called a "half-adder" circuit. It takes two input bits A and B and produces two outputs A XOR B and A AND B, which equate to the SUM bit and CARRY bit respectively. When adding two binary representations, one travels from right to left and at each step, one adds the bits to the previously carried bit and then records the sum of the bits and carries over any overflowing bit to the next step. So at each step, you have 3 inputs, namely the previously carried bit (called Cin) and the two bits A and B, and two outputs namely the SUM of A and B and a carried over bit (called Cout). To handle all the cases involved in this scenario one uses the "full-adder" circuit as shown below. It's easy to verify that the full adder circuit handles all the cases involved in adding the three bits Cin, A, and B. 

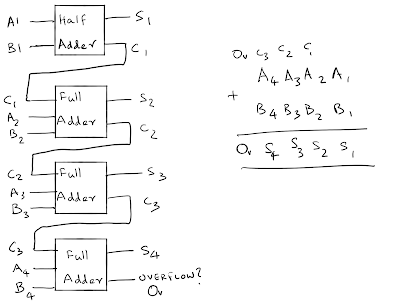
Arbitrary integer addition can be performed by stacking a half-adder on top of a stack of full-adders and passing on the carry output of each addere as the carry input to the next adder below and accounting for any overflow in the end. 

Similarly, other arithmetic operations can be performed using algorithms that ultimately boil down to logic circuits. For example, a recursive scheme called the Karatsuba algorithm is used to efficiently multiply large integers using products of smaller integers, which in turn can be multiplied using logic circuits such as the ones discussed above. We will discuss the Karatsuba algorithm when we discuss integer factoring and Shor's algorithm in a later post. In addition to integers, other data structures such as characters, floating-point numbers, images, file systems, and memory addresses are all ultimately represented using arrays of bits. In many cases, integers themselves are used such as code points for ASCII and Unicode characters and RBG values for images. Often various forms of encoding (such as UTF-8) are used to convert the data structures into bit arrays when writing out data into files or transmitting data across a network. Bit operations perform a crucial role in manipulating these data structures. In fact, much of modern cryptography relies on bit operations and integer arithmetic. For example, the "one-time pad" is a provably secure algorithm for performing one-time encryption of a given string of characters and it is based on the XOR operation.

Logic circuits are fundamental for modern computing. It turns out that the circuit model of computing extends to quantum computing as well and is essential for implementing quantum algorithms. In fact, classical circuits can be extended to reversible quantum circuits and are used in all the famous quantum algorithms. We will see how quantum circuits are built and used in the next post on quantum computing.

Qubits

The qubit is a dramatic generalization of the classical notion of a bit. A bit is an abstract representation of a 2-state system that one often encounters in daily life. For example, a light bulb is a 2-state system that can be on or off, a transistor is a 2-state system that can be on or off resulting in current flowing or not, a spinning top is a 2-state system that can be spinning clockwise or counter-clockwise and a cat is a 2-state system that is either dead or alive. But there are many 2-state systems studied in physics that have a ghostly nature that follow the strange rules of quantum mechanics. A qubit is similar to a bit in that it is a 2-state system when measured, meaning it can take only one of two possible values 0 or 1. However, when a qubit is not measured its evolution is based on rules of quantum mechanics that state that it is in a linear superposition of the 0 and 1 states. A system that is in superposition is in both 0 and 1 states simultaneously with a certain proportion. The squares of these proportions represent probabilities. The following diagram motivates the concept of a qubit. 

A bit can have two possible values 0 or 1. These are represented above using two red dots. Now replace the dots with vectors of length 1 where an "up" vector represents 0 and a "down" vector represents 1. Now to rotate this unit vector in 3-dimensional space. The endpoints of the vectors will reside on a unit sphere known as the "Bloch sphere".  A qubit refers to a point on the surface of this sphere. This is the state of the qubit when it is not measured. It turns out that one can express a point on the Bloch sphere as a "complex linear combination" of the up and down vectors. Here complex means a number of the form "a + b i" where "i" is the square root of -1 and a and b are real numbers.  The up and down vectors are called "basis states" and the vector representing a point on the unit sphere represents an arbitrary qubit state. Therefore a qubit can be expressed as a complex vector "c |0> + d |1>"  where c and d are complex numbers and |0> and |1> represent the "up" and "down" basis vectors respectively. One can prepare a qubit in a certain state. For example, a qubit could start out as the "up" arrow (|0> state) and then undergo transformations to assume a different state on the Bloch sphere. If the transformations are known then the qubit state and the associated coefficients c and d are also known. However, the coefficients can never be measured. This is the famous quantum indeterminism. The coefficients c and d represent the "private world" of the qubit. When a qubit is measured, it undergoes an irreversible disturbance that causes the state to collapse to |0> or |1> with the probabilities given by the absolute square of the coefficients. If we were to sample identical qubits by measuring them, one could estimate the probabilities, but one can never measure the "inner state" of the qubit.  

There are many 2-state systems in nature that behave in this way and can be represented by qubits. Some well-known examples are currents flowing through superconducting wires at very low temperatures, magnetic spins of charged particles, energy levels of trapped ions, and the polarization modes of photons. To understand qubits in their full generality one has to review the properties of complex numbers and vectors. Most of the literature on quantum information (and there is plenty out there) starts with the Bloch sphere and the most general complex representation of a qubit. To the initiated casual reader it can be a little daunting to read at first. However, it turns out that one can understand a lot about qubits using just high school trigonometry by focusing on "real-valued" qubits. In fact, most of the concepts of quantum information can be understood using this simpler flavor of qubits. Some of the most important algorithms in quantum information such as the Deutsch-Jozsa algorithm, Bernstein-Vazirani algorithm, Simon's algorithm, Quantum Key Distribution (QKD), and Quantum Teleportation algorithms can be understood using just real-valued qubits. Moreover, there is a concrete physical realization of real-valued qubits namely the linear polarization of a photon of light. It provides a perfect illustration of the key aspects of a qubit without requiring an understanding of complex numbers and linear algebra. In fact, when we do discuss complex-valued qubits we will use circular polarization of a light photon to illustrate the more advanced aspects of qubits. Eventually to understand the crown jewels of quantum computing such as Shor's algorithm, the Quantum Fourier Transform, and Grover's algorithm we will need to work with complex-valued qubits. But in this post, we will focus only on real-valued qubits and discuss complex-valued qubits only when we need them in the next post. Here is a diagram that was drawn by my 17-year old daughter to help my 14-year old son understand the basics of trigonometry. It will be essential for our discussion of real-valued qubits.

by Tanvi Adhikari

A real-valued qubit can be represented by just a point on the unit circle as shown below. The point (1,0) on the X-axis is labeled |0> and the point (0,1) on the Y-axis is labeled |1>.  A qubit is an arbitrary point on the circle whose values can be expressed in terms of the angle of the vector with respect to the X-axis. The point can also be expressed as a linear combination of |0> and |1> as shown below.

The state of a qubit is always expressed in terms of a measurement basis. Any pair of orthogonal unit vectors can serve as a basis for representing qubits. The vectors represented by |0> and |1> are orthogonal to each other and are together called the "computational basis". The state |0> represents a qubit whose measured value with respect to the computational basis is always 0, and the state |1> represents a qubit whose measured value with respect to the same basis is always 1. When an arbitrary qubit is measured in the computational basis its value is 0 or 1 with a probability given by the square of the coefficient of |0> or |1> (which are respectively the square of the cosine and sine of the angle of the qubit vector with respect to the X-axis as shown above). Therefore the probabilities of obtaining 0 or 1 are given by the squares of the cosine and sine respectively. When a measurement is performed on the qubit, the state of the qubit "collapses" to |0> or |1> with the same respective probabilities.

Since the probability of a measurement outcome in a basis is the square of the linear coefficient of the qubit state with respect to the basis, we get the following conclusions:

• Measurement of |0> with respect to the computational basis leaves the qubit in the state |0> and produces a value of 0 with 100% probability. The analogous statement is true for the measurement of the qubit state |1> with respect to the computational basis.
• Measurement of the qubit states |+> or |-> with respect to the computational basis collapses the state to |0> or |1> with a probability of 1/2 (50%) and the measured value is 0 or 1 respectively.
• One can measure a qubit state with respect to a "rotated basis" such as the +- basis. Measuring the state |0> or |1> with respect to the +- basis will collapse the state to |+> or |-> with a 50% probability each. Therefore, even though measuring a state like |0> in the computational basis produces an outcome of |0> will 100% probability, measuring it on a rotating basis disturbs it irreversibly and produces an indeterminate value of + or - with 50% probability. This is the uncertainty principle in action. 
• This phenomenon of certainties becoming probabilities when measured on a different basis is a crucial aspect of quantum mechanics and plays an important role in security protocols such as quantum key distribution.

Photon Polarization

Linear polarization of light provides a perfect illustration of qubit states. The wave-particle duality of light (and matter) is a fundamental principle of quantum mechanics. Light consists of electromagnetic waves. The polarization of light refers to the direction of oscillation of the electrical and magnetic fields on the plane perpendicular to the direction of propagation of lightwave (represented by the wave vector). A horizontally polarized light wave has its electric field oscillating along the X-axis (and the magnetic field along the Y-axis) based on a chosen X-Y coordinate system perpendicular to the wave vector. Similarly, a vertically polarized light wave will have its electrical field oscillating in the Y-axis (and the magnetic field along the X-axis) with respect to the chosen X-Y coordinate system. A horizontal polarizer will allow only horizontally polarized light and block vertically polarized light and vice versa. This can be demonstrated by putting a vertical polarizer behind a horizontal polarizer and sending in a light beam. No light will go through because the light coming out of the horizontal polarizer is horizontally polarized, which is blocked by the vertical polarizer. So far so good. But things get interesting if you place a polarizer between the horizontal and vertical polarizers that is parallel to the polarizers but rotated at an angle to the X-axis. While one would expect the light to be still blocked, it turns out that now actually a portion of the light is allowed to go through and the proportion of the light intensity that goes through is given by the square of the cosine of the angle between the inclined polarizer and the X-axis. The amount of light blocked is the square of the sine of the angle.  

But light also consists of quanta of energy known as photons. The intensity of light is proportional to the number of photons going through a perpendicular surface area. Then one can explain the transmission or blocking of the light through the inclined polarizer in terms of the probability that a photon is allowed to go through or the probability that it blocked by the inclined polarizer. A photon that is allowed to go through would be said to be polarized in the inclined direction and a photon that is blocked can be thought of as polarized in a direction perpendicular to the axis of inclination. Since the intensity of light that goes through is proportional to the square of the cosine of the angle of the direction of polarization with the X-axis it follows that the probability of a photon going through is the square of the cosine of the angle of inclination and the probability of being blocked is the square of the sine of the angle of inclination. This provides us with some evidence that the polarization mode of a photon could be represented by a qubit. The quantum theory of a photon posits that the polarization mode of light is based on the spin of the photon (which is a boson) which is in fact a qubit. In fact, quantum security protocols such as quantum key distribution (QKD) make use of photonic qubits to securely share cryptographic keys.  

Entanglement

Arguably the most intriguing aspect of qubits is their ability to get entangled with each other. When two qubits are independent and don't interact with each other their combined state can be expressed in terms of the individual states as a tensor product of the two states. This is shown below. The computational basis for a two-qubit system is just the set of all 2-bit strings - (|00>, |01>, |10>, |11>. The most general state of a 2-qubit system is a linear superposition of the basis states. As shown below this includes states like the Bell states that cannot be separated into a tensor product of their individual qubit states. 

When two qubits are entangled with each other just knowing the states of the individual qubits is not sufficient to know the state of the combined pair of qubits. Thus the whole is greater than the sum of its parts. Thus the pair of qubits must be treated as a single system.  Moreover, even though the measurement outcome of each of the qubits is non-deterministic, the measurement outcomes are strongly correlated with each other. For example, in the first two Bell states measurement of each qubit will produce a 0 or 1 with 50% probability. But if the measurement outcome of one of the qubits is 0 then the measurement outcome of the other qubit is also 0. Alternatively, if the measurement outcome of one qubit is 1 then the measurement outcome of the other has to be 1. It appears as though when one of the qubits is measured it instantaneously forces the state of the other qubit to be one or the other based on the first qubit's measurement outcome. This happens no matter how far the individual qubits are from each other in space. This is what Einstein referred to as "spooky action at a distance". Einstein believed that if one qubit could influence the other qubit instantaneously that would constitute a violation of the special theory of relativity. Therefore, he claimed in the famous EPR paper that quantum theory was an incomplete theory of nature. A complete theory of nature would account for "hidden variables" that explain the correlations between the measurement outcomes of the two qubits. Einstein's objection was based on a philosophical assumption called "local realism". Local realism posits that faraway events can’t influence each other faster than the speed of light (“locality”) and properties of objects have a definite value even if we don’t measure them (“realism”). It turns out that by Bell's theorem local realism is incompatible with quantum theory.

Entanglement is a fundamental characteristic of quantum mechanics and has been observed in many systems across large distances. For example, the light going through certain types of crystals called "nonlinear crystals" can produce linearly polarized photon pairs whose polarization states are entangled with each other.

In subsequent posts, we will discuss Bell's theorem, quantum communication, quantum gates, quantum circuits, and their application to quantum computation.